Statistics : Linear Regression made easy !!

A Simple Linear Regression is a straight line relationship between dependent and independent variable.




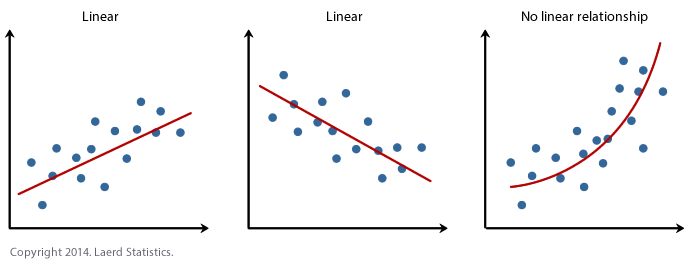
The above diagram describes, fitting a straight line to describe the relation between two variables. The points on the graph are randomly chosen observations of the two variables. The straight line describes the general movement of the data - an increase in Y(dependent) corresponding to an increase in X(independent). An inverse straight line relationship is also possible.

Simple Linear Regression Model:

Model must contain two parameters i.e. population intercept and population slope.

The method that will give us good estimates of the regression coefficients is the method of least squares.

We should come up with a line that is best fit with the data points and minimizes the errors i.e. we should minimize the sum of squared errors (SSE as in ANOVA)

Below are few formulas for calculating SSE, bo and b1.

Note:

Y is the dependent  and X is the independent variable

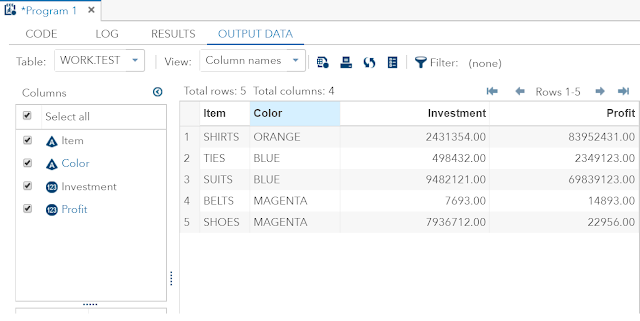
Example:

A study was conducted to determine the relation between travel(X) and charges(Y) on American Express card as they believe that their cardholders use their card most extensively than other cards.

Below is the data:

• X and Y are Miles and Dollars respectively. 
• X square , Y square and XY for easy calculation. 

Let us see the manual calculation for building the linear regression model i.e. Y=bo + b1X

Our model is Y=274.85 + 1.26X

Let us check the same in tools like SAS and R

SAS

Below is the code and the output which gives the same result as manual calculation

Code:

FILENAME REFFILE '/home/test/linear_reg_data.xlsx';

PROC IMPORT DATAFILE=REFFILE

DBMS=XLSX

OUT=WORK.IMPORT;

GETNAMES=YES;

RUN;

proc reg data=import;

model dollars=miles;

run;

Output:

R Studio

Code

library(readxl)

linear_reg_data <- read_excel("C:/Users/pc/Desktop/linear_reg_data.xlsx")

View(linear_reg_data)

plot(dollars~miles, data=linear_reg_data)

model1=lm(dollars~miles,data=linear_reg_data)

summary(model1)

Output:

Call:

lm(formula = dollars ~ miles, data = linear_reg_data)

Residuals:

    Min      1Q      Median      3Q     Max 

-588.79 -263.96   63.52     200.68  498.66 

Coefficients:

                    Estimate     Std. Error    t value    Pr(>|t|)    

(Intercept) 274.84969    170.33684   1.614      0.12    

miles         1.25533        0.04972       25.248   <2e-16 ***

---

Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 318.2 on 23 degrees of freedom

Multiple R-squared:  0.9652, Adjusted R-squared:  0.9637 

F-statistic: 637.5 on 1 and 23 DF,  p-value: < 2.2e-16

The model is same in all the tools and manual calculation 😊😊

SAS Example : Daily Sales Report Automation

The purpose of this post is to give an idea on automation of report generation. 

The below code generates Automated Sales Summary Email based on discrete sales figures on a product, place, cost & revenue by utilizing macros.

Create a sample sales data as below:

data sales;
input product_id place $ product_cost product_revenue ;
date=today()-1;format date date9.;
cards;
101 goa 100 200
101 punjab 100 250
101 mumbai 100 300
101 chennai 100 175
101 kerala 100 225
102 goa 200 400
102 punjab 200 450
102 mumbai 200 400
102 chennai 200 475
102 kerala 200 425
;
run;

SAS dataset:

Macro to generate sales report daily:

The SAS macro generates the sales stats and sends an email automatically without manual intervention.


%macro sales_report();

/* macro variable to capture yesterday's date*/
%let date=%sysfunc(putn(%eval(%sysfunc(today())-1),date9.));
%put &date.;

/* filter yesterday's sales data*/
data sales_fltr;
set sales;
where date="&date."d;
run;

/* Mention email id to which the report has to be generated. Modify the subject if required */

   filename temp email to="your_email@gmail.com"
            subject="Sales report - &date. "
            type="text/html";

   ods html body=temp;

   proc sql;
   select product_id,
    sum(product_cost) as total_cost,
    sum(product_revenue) as total_revenue,
    calculated total_revenue-calculated total_cost as profit
   from sales_fltr
   group by product_id;
   run;

   ods html close;

%mend;
%sales_report;

Email:

SAS output:

SAS Example : List the missing percentage of variables/columns of dataset

This post lists the missing percentage of all the variables in a dataset.

Below code to create sample data:

data sample;
input id name $;
cards;
1 anil
2 bob
3 arun
4 tarun
5 tom
5 paul
7 peter
8 krish
9 sai
10 gita
;
run;

Assign missing values. (name has 2 missing values and id has 1 missing value)

data sample1;
set sample;
if id>=9 then name='';
if name='tom' then id=.;
run;

Macro:

Below macro lists the missing percentage of variables in a dataset.

%macro list_misspct(input_dataset);

proc contents data = &input_dataset out = var_list noprint;
run;

proc sql noprint;
select count(*) into :total_obs from &input_dataset;
select count(*) into :var_cnt from var_list;
select name into :var_in separated by ' ' from var_list;
select type into :var_type separated by ' ' from var_list;
quit;

/*Creating dataset to hold variable names and their missing percentages*/

proc sql noprint; 
CREATE TABLE misspercentage
(Variable varchar(32),
missing_percentage int);
quit;

/*Computing missing percentage of variables*/

%do i=1 %to &var_cnt;

%let scan_var=%scan(&var_in,&i);
%let scan_type=%scan(&var_type,&i);

proc sql noprint;
create table miss_pct as
select "&scan_var" as variable,
sum(case when &scan_var is missing then 1 else 0 end) as miss_cnt,
((calculated miss_cnt/&total_obs)*100) as missing_percentage
from &input_dataset;
quit;

proc append base=misspercentage data=miss_pct(keep=variable missing_percentage) force;
run;

%end;

proc print data=misspercentage;run;

%mend list_misspct;

%list_misspct(sample1);

Note: Missing percentage calculation: count of missing observations/total no. of observation

Free SAS Tutorials: Dataset creation

Dataset

SAS dataset is generally in the form of table, i.e rows and columns. In SAS, rows are called observations and columns as variables.

Dataset creation

Below statements are used for creating a dataset:

• DATA -  The DATA step always begins with a DATA statement. The purpose of the DATA statement is to tell SAS that you are creating a new data set i.e. outdata.
• INPUT -  To define the variables used in data set.
• Dollar sign ($) - To identify variable as character.
• DATALINES - To indicate that lines following DATALINES statement a real data.
• RUN - The DATA step ends with a RUN statement.

Example 1:

Data datasetname;

     input var1 var2 $;

     datalines;

      1 anil

      2 raj

      3 ravi

      4 neetu

      ;

run; 

Code:

Output:

Example 2:

data Test;    

input Item $ 1-6 Color $ 8-14 Investment 16-22 Profit 24-31;    

format Item Color $9. Investment  Profit  15.2;     

datalines; 

SHIRTS ORANGE  2431354 83952431 

TIES   BLUE    498432  2349123 

SUITS  BLUE    9482121 69839123 

BELTS  MAGENTA 7693    14893 

SHOES  MAGENTA 7936712 22956 

; 

run;

The highlighted input statement is another way of creating the variables by mentioning the position numbers.

Code:

Output:

Datasets are of 2 types: Temporary and Permanent

Temporary dataset:

These datasets are not available after the session is closed or ended. Usually they are saved in work library(a storage location where sas datasets are saved). 

The below 2 statements are equivalent.

data work.sample;

or

data sample;

Permanent dataset:

These datasets are saved in a location which can be used even after closing the sas session. Usually, these datasets are referenced as libref.dataset_name. Libref is a name that is temporarily assigned to a library. Library is storage where all the sas datasets are saved. 

A LIBNAME statement associates the libref with the SAS library. In the following PROC PRINT step, PROCLIB is the library reference and EMP is the SAS data set within the library:

libname proclib 'SAS-library';
proc print data=proclib.emp;
run;

Dataset creation using PROC SQL:

Proc SQL can be used for creating a dataset by connecting to Oracle database or from existing dataset.

Example: Creation of dataset sample from existing dataset i.e sashelp.cars

Proc sql;

create table sample as

select * from sashelp.cars;

quit;

SAS Example : Split dataset into n equally sized datasets

Considering the cars dataset available in sashelp and splitting it to 10 equally sized datasets.

Step1:

Creating a row number using _n_ system variable option.
           
               data sample;
                   set sashelp.cars;
                        n=_n_;
               run;

Step2:

The below macro splits the data into n equally sized datasets. n is passed as a parameter to the macro.

• Macro name : split

• creating a cnt macro variable which holds the no. of observation count of the cars dataset. Cars dataset has 428 observations, therefore cnt = 428 

• number macro variable holds the no. of observations to be kept in each split dataset. In the below macro, cars dataset is split into 10 datasets. therefore number = 428/10 ~ 43 observations 

• DO loop to iterate 10 times to split the cars dataset into 10 equally sized datasets. The split datasets are named as sample_1 to sample_10.

%macro split(divide);

         proc sql;
               select max(n) into :cnt from sample;
         quit;

         data split;
               num=ceil(&cnt/&divide);
         run;

         proc sql;
               select num into :number from split;
         quit;

         %do i=1 %to &divide;

                data sample_&i;
                     set sample;
                          if n>=((&i-1)*&number)+1 and n<=(&i*&number);
                run;

        %end;

%mend split;

%split(10);

Code:

Output:

Statistics : Basics - Mean , Median and Mode

Arithmetic mean/Mean

It is the most common measure of central tendency. It serves as a balance point in a set of data. It is the only common measure in which all the values play an equal role. Mean is computed as sum of all the values divided by number of values in the data set. It is denoted by X-bar.

Example:

Age of students in class:

12 13 12 11 14 15 12 13 14

Mean=  ( 12 + 13 + 12 + 11 + 14 + 15 + 12 + 13 +14 ) / 9 = 116 / 9 = 12.88

Therefore, the average age is 12.8 ~ 13years

Median

Median is the middle value in an ordered array of the data that has been ranked from smallest to the largest. Half of the values are smaller or equal to the median, and half of the values are larger or equal to the median. In case of extreme values, median can be used as it is not affected.

Median has different calculation in case of odd and even data numbers.

Odd number of values

Median is the middle value of the sorted data

Example:

Age of students in class: 12 13 12 11 14 15 12 13 14

First sort the data : 11 12 12 12 13 13 14 14 15

Therefore, Median is 13

Even number of values

Median is the average of two middle values of the sorted data

Example:

Age of students in class: 12 13 12 11 14 15 12 13 14  12

First sort the data : 11 12 12 12 12 13 13 14 14 15 

Median = (12 + 13) /2 =12.5

Mode

Mode is the value that appears most frequently. Like the median and unlike the mean, it is not affected by the extreme values. For a particular variable, there can be several modes or no modes at all.

Example:

Age of students in class: 12 13 12 11 14 15 12 13 14 13

Since 12 and 13 has occurred 3 times, mode :12 & 13.

Comparison of Mean , Median and Mode

The determination of which average exactly suits for a specific variable depends on many factors. Certainly depends on the data level. Below are the valid averages for each level of data.

Nominal data => Mode

                   Ordinal data   => Mode and Median

                               Interval data  => Mean, Median and Mode 

                              Ratio data      => Mean, Median and Mode

For a symmetrical distribution, all the three measures  mean, median and mode are exactly same in value.

i.e, Mean = Median = Mode

Geometric Mean

When you want to measure the rate of change of the variable over time, you need to use the geometric mean instead of arithmetic mean. It is computed as nth root of product of n values.

Harmonic Mean

It is also a mathematical average. It is the reciprocal of the average of  the reciprocal of the values i.e number of values divided by sum of its reciprocals.

Example:

The time taken by 3 teams for designing a caption are 6,3 and 8min. For computing the average rate of designing the caption is

XH= 3 / (1/6 + 1/3 + 1/8) = 3/(15/24) = 24/5 = 4.8min

Arithmetic mean would be X=6+3+8/3 = 5.6min

Harmonic mean will always be less than arithmetic mean.

Free SAS Tutorials : Basics of SAS programming

SAS stands for STATISTICAL ANALYSIS SYSTEM

SAS software (Click here for free SAS software access)

SAS has 3 windows:

1. Editor/code window : A place where we write our codes/programs.
2. Log window : All the executed SAS codes are printed in this window along with any error or warning messages. A PUT statement can be used to print the output in the log window.
3. Output window(non default window) : Appears only where there is an output from the sas program mostly whenever a dataset is created(dataset is a sas file which has data in the form of rows(observations) and columns(variables)).
4. Result window : Place where we can see the result from the sas code which is only viewed but is not saved.

Editor/code window

Log window

Output window

How does a SAS data looks like?

A SAS data set contains data values that are organized as a table of observations (rows) and variables (columns) that can be processed by SAS software.

The below image has 4 variables i.e, name, age, height and weight and 3 observations.

SAS Components

•  Base SAS – Basic procedures and data management 
•  SAS/STAT – Statistical analysis 
•  SAS/GRAPH – Graphics and presentation 
•  SAS/ETS – Econometrics and Time Series Analysis 
•  SAS/INSIGHT – Data mining 
•  Enterprise Miner – data mining 
•  Enterprise Guide - GUI based code editor & project manager 
•  SAS EBI - Suite of Business Intelligence Applications 

Basic SAS programming guidelines:

1. Each statement ends with a semicolon.
• Example: Data sample; Input id;
2. A single statement can be written in multiple lines or multiple sas statements can be written in single line.
3. SAS statements are not case sensitive.
4. Every data step and proc step should end with RUN statement and proc sql should end with QUIT statement
• Example - data step: Data sample;var1=10;run;
• Example - proc step: proc print data=sample;run;
• Example - proc sql;select * from sample;quit;
5. All the sas variable names should be between 1 to 32 characters.
6. SAS variable names can start with a underscore (_) or character but cannot start with number. Blank spaces and few special characters like $,%, & are not allowed in the variable names.
7. SAS code comments are specified in two ways. 
• commenting starts with  asterisk(*) and ends with semicolon(;) --- * comment ;
• Example: 
• * mention the comments;
• * comment line 1

                              * comment line 2;

• commenting starts with /* and ends with  */ --- /* comment */
• Example:

                              /* comment line 1
                                  comment line2

                                  comment line 3 */

SAS Programming:

Every sas code starts with either a DATA step or PROC step

DATA step

• Data step starts with keyword DATA and ends with RUN statement
• One of the way to create a dataset
• Data step is used to get the data from a raw file like excel ,text etc. 
• It is used to manage the data, create new variables, transform the data.
• Create variables and observations

Sample code:

Output:

PROC step

• Proc step starts with keyword PROC and end with RUN statement.
• Proc steps are nothing but inbuilt procedures available in SAS. 
• These are used to analyze the data, view the data and generate reports.

Sample code:

Output:

<- Previous